Here you will learn about recursive formulas, including what they are and how to write them.
Students will first learn about recursive formulas as part of functions in high school.
The recursive formula is an equation that uses recursion to relate terms in a sequence. Recursion uses a rule over and over again. This relationship can be used to find the next term or the previous term.
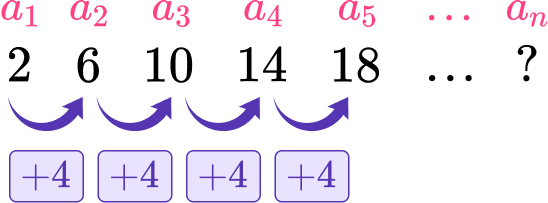
Each number in a sequence is called a term, and each term is identified by its position within the sequence. For this sequence, the difference from term to term is common, making it an arithmetic sequence. You can write the first few terms as,
The first term, a_1=2
The second term, a_2=6
The third term, a_3=10
The fourth term, a_4=14
The fifth term, a_5=18
The n th term, a_n
The next term, a_
One way of generating this sequence would be to use a recursive formula, where each term is generated using the previous value.
When n=3, a_3=6+4=10, and so on.
So, the recursive formula is written as a_=a_n+4.
The initial value, a_1, would need to be provided. The initial value could also be a_0.
Recursive formulas can be used to find particular solutions, but require starting at the beginning and repeatedly applying the rule to each term until the desired term is reached.
Another way of generating this sequence would be to use an explicit formula, which defines the relationship between the terms position and the value of the term itself.
To generate this sequence you can use the explicit formula for the sequence. For this sequence, the nth term would be a_n=2+4(n-1).
When n=1, a_1=2+4(0)=2.
When n=2, a_2=2+4(1)=6, and so on.
Step-by-step guide: Explicit formula
The following sequence of numbers is a special type of recursive sequence called the Fibonacci sequence.
1, 1, 2, 3, 5, 8, 13, 21, …
The next number of the sequence can be found by adding the two previous terms together. Therefore, the Fibonacci numbers can be written using a recursive formula. You need to be given the first 2 numbers in the Fibonacci sequence.
If you change the first 2 values, you can generate a different Fibonacci sequence.
For example, F_=F_+F_n, \, F_1=2, \, F_2=5
would give the sequence 2, 5, 7, 12, 19, 31, …
In general, a Fibonacci sequence can be written as, F_=F_+F_n, \, F_1=a, \, F_2=b
and would give the sequence a, \, b, \, a+b, \, a+2b, \, 2a+3b, \, 3a+5b, …
Did you know the Fibonnaci numbers occur often in nature? Flowers often have 3 or 5 or 8 petals. This is why a clover with 4 petals is difficult to find and is considered lucky.
How does this relate to high school math?
![[FREE] Number Patterns Check for Understanding Quiz (Grade 4 to 5)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Number-patterns-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 5 students’ understanding of number patterns. 10+ questions with answers covering a range of 4th and 5th grade number patterns topics to identify areas of strength and support!
Use this quiz to check your grade 4 to 5 students’ understanding of number patterns. 10+ questions with answers covering a range of 4th and 5th grade number patterns topics to identify areas of strength and support!
In order to generate a sequence using a recursive formula:
A sequence is defined by a recursive formula a_=a_n-4 and has a_0=100.
Find the next four terms of the sequence.
The recursive formula is given in the question, a_=a_n-4.
2 Substitute the given initial value into the formula to calculate the new value, \bf+1>>.
The initial value is given in the question, a_0=100.
Substituting this into a recursive formula gives a_1=a_0-4=100-4=96.
4 Repeat step \bf until the desired number of terms has been generated.
\begin & a_3=a_2-4=92-4=88 \\\\ & a_4=a_3-4=88-4=84 \end
The next four terms of the sequence are 96, 92, 88 and 84.
A sequence is defined by a recursive formula a_=5 a_n and has a_0=1.
Find the next four terms of the sequence.
Find a recursive formula.
The recursive formula is given in the question, a_=5 a_n
Substitute the given initial value into the formula to calculate the new value, \bf+1>>.
The initial value is given in the question, a_0=1.
Substituting this into a recursive formula gives a_1=5 a_0=5 \times 1=5.
a_2=5 a_1=5 \times 5=25Repeat step \bf until the desired number of terms has been generated.
\begin & a_3=5 a_2=5 \times 25=125 \\\\ & a_4=5 a_3=5 \times 125=625 \endThe next four terms of the sequence are 5, 25, 125, 625.
In order to find a recursive formula of a sequence:
Find a recursive formula that satisfies the sequence 5, 8, 11, 14, 17, …
Find the arithmetic or geometric relationship linking the terms.
Each term in this sequence is 3 more than the one before it.
Write a recursive formula with correct notation.
The recursive formula is written as a_=a_n+3.
Give one term of the sequence as well as a recursive formula.
The description needs to be more specific, so giving one term in the sequence, as well as a recursive formula is written as
Write down a recursive formula which produces the sequence 3, 6, 12, 24, 48, …
Find the arithmetic or geometric relationship linking the terms.
Each term in this sequence is double the previous term.
Write a recursive formula with correct notation.
The recursive formula is written as a_=2a_n.
Give one term of the sequence as well as a recursive formula.
The description needs to be more specific, so giving one term in the sequence, as well as a recursive formula is written as,
Describe the sequence 32, 37, 42, 47, … using a recursive formula.
Find the arithmetic or geometric relationship linking the terms.
Each term in this sequence equals the one before it, plus 5.
Write a recursive formula with correct notation.
The recursive formula is written as a_=a_n+5.
Give one term of the sequence as well as a recursive formula.
The description needs to be more specific, so giving one term in the sequence, as well as a recursive formula is written as
Write down a recursive formula which produces the sequence 20, –10, 5, –2.5, 1.25, …
Find the arithmetic or geometric relationship linking the terms.
Each term in this sequence is half the previous term. The terms also alternate between positive and negative.
Write a recursive formula with correct notation.
The recursive formula is written as a_=-\cfrac \, a_n.
Give one term of the sequence as well as a recursive formula.
The description needs to be more specific, so giving one term in the sequence, as well as a recursive formula is written as
For example,
The first term of the sequence should always be defined, and is often a_1.
If a_1 is the first term, then a_2 is the second term, and so on with all successive terms. a_n is the n th term, a_ is the next term, and a_ is the preceding term.
